The roles of computer programs in science
Why do people write computer programs? The answer seems obvious: in order to produce useful tools that help them (or their clients) do whatever they want to do. That answer is clearly an oversimplification. Some people write programs just for the fun of it, for example. But when we replace "people" by "scientists", and limit ourselves to the scientists' professional activities, we get a
statement that rings true: Scientists write programs because these programs do useful work for them. Lengthy computations, for example, or visualization of complex data.
This perspective of "software as a tool for doing research" is so pervasive in computational science that it is hardly ever expressed. Many scientists even see software, or perhaps the combination of computer hardware plus software as just another piece of lab equipment. A nice illustration is this TEDx lecture by Klaus Schulten about his "computational microscope", which is in fact Molecular Dynamics simulation software for studying biological macromolecules such as proteins or DNA.
To see the fallacy behind equating computer programs with lab equipment, let's take a step back and look at the basic principles of science. The ultimate goal of science is to develop an understanding of the universe that we inhabit. The specificity of science (compared to other approaches such as philosophy or religion) is that it constructs precise models for natural phenomena that it validates and improves by repeated confrontation with observations made on the real thing:
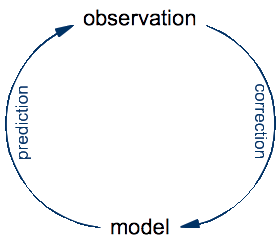
An experiment is just an optimization: it's a setup designed for making a very specific kind of observation that might be difficult or impossible to make by just looking at the world around us. The process of doing science is an eternal cycle: the model is used to make predictions of yet-to-make observations, whereas the real observations are compared to these predictions in order to validate the model and, in case of a significant discrepancies, to correct it.
In this cycle of prediction and observation, the role of a traditional microscope is to help make observations of what happens in nature. In contrast, the role of Schulten's computational microscope is to make predictions from a theoretical model. Once you think about this for a while, it seems obvious. To make observations on a protein, you need to have that protein. A real one, made of real atoms. There is no protein anywhere in a computer, so a computer cannot do observations on proteins, no matter which software is being run on it. What you look at with the computational microscope is not a protein, but a model of a protein. If you actually watch Klaus Schulten's video to the end, you will see that this distinction is made at some point, although not as clearly as I think it should be.
So it seems that the term "a tool for exploring a theoretical model" is a good description of a simulation program. And in fact that's what early simulation programs were. The direct ancestors of Schulten's computational microscope are the first Molecular Dynamics simulation programs made for atomic liquids. A classic reference is Rahman's 1964 paper on the simulation of liquid argon. The papers of that time specify the model in terms of a few mathematical equations plus a some numerical parameters. Molecular Dynamics is basically Newton's equations of motion, discretized for numerical integration, plus a simple model for the interactions between the atoms, known as the Lennard-Jones potential. A simulation program of the time was a rather straightforward translation of the equations into FORTRAN, plus some bookkeeping and I/O code. It was indeed a tool for exploring a theoretical model.
Since then, computer simulation has been applied to ever bigger and ever more complex systems. The examples shown by Klaus Schulten in his video represent the state of the art: assemblies of biological macromolecules, consisting of millions of atoms. The theoretical model for these systems is still a discretized version of Newton's equations plus a model for the interactions. But this model for the interactions has become extremely complex. So complex in fact that nobody bothers to write it down any more. It's not even clear how you would write it down, since standard mathematical notation is no longer adequate for the task. A full specification requires some algorithms and a database of chemical information. Specific aspects of model construction have been discussed at length in the scientific literature (for example how best to describe electrostatic interactions), but a complete and precise specification of the model used in a simulation-based study is never provided.
The evolution from simple simulations (liquid argon) to complex ones (assemblies of macromolecules) looks superficially like a quantitative change, but there is in fact a qualitative difference: for today's complex simulations, the computer program is the model. Questions such as "Does program X correctly implement model A?", a question that made perfect sense in the 1960s, have become meaningless. Instead, we can only ask "Does program X implement the same model as program Y?", but that question is impossible to answer in practice. The reason is that the programs are even more complex than the models, because they also deal with purely practical issues such as optimization, parallelization, I/O, etc. This phenomenon is not limited to Molecular Dynamics simulations. The transition from mathematical models to computational models, which can only be expressed in the form of computer programs, is happening in many branches of science. However, scientists are slow to recognize what is happening, and I think that is one reason for the frequent misidentification of software as experimental equipment. Once a theoretical model is complex and drowned in even more complex software, it acquires many of the characteristics of experiments. Like a sample in an experiment, it cannot be known exactly, it can only be studied by observing its behavior. Moreover, these observations are associated with systematic and statistical errors resulting from numerical issues that frequently even the program authors don't fully understand.
From my point of view (I am a theoretical physicist), this situation is not acceptable. Models play a central role in science, in particular in theoretical science. Anyone claiming to be theoretician should be able to state precisely which models he/she is using. Differences between models, and approximations to them, must be discussed in scientific studies. A prerequisite is that the models can be written down in a human-readable form. Computational models are here to stay, meaning that computer programs as models will become part of the daily bread of theoreticians. What we will have to develop is notations and techniques that permit a separation of the model aspect of a program from all the other aspects, such as optimization, parallelization, and I/O handling. I have presented some ideas for reaching this goal in this article (click here for a free copy of the issue containing it, it's on page 77), but a lot of details remain to be worked out.
The idea of programs as a notation for models is not new. It has been discussed in the context of education, for example in this paper by Gerald Sussman and Jack Wisdom, as well as in their book that presents classical mechanics in a form directly executable on a computer. The constraint of executability imposed by computer programs forces scientists to remove any ambiguities from their models. The idea is that if you can run it on your computer, it's completely specified. Sussman and Wisdom actually designed a specialized programming language for this purpose. They say it's Scheme, which is technically correct, but Scheme is a member of the Lisp family of extensible programming languages, and the extensions written by Sussman and Wisdom are highly non-trivial, to the point of including a special-purpose computer algebra system.
For the specific example that I have used above, Molecular Dynamics simulations of proteins, the model is based on classical mechanics and it should thus be possible to use the language of Sussman and Wisdom to write down a complete specification. Deriving an efficient simulation program from such a model should also be possible, but requires significant research and devlopment effort.
However, any progress in this direction can happen only when the computational science community takes a step back from its everyday occupations (producing ever more efficient tools for running ever bigger simulations on ever bigger computers) and starts thinking about the place that it occupies in the pursuit of scientific research.
Update (2014-5-26) I have also written a more detailed article on this subject.